Sorting is a fundamental problem in computer science. It refers to the process of arranging data in a specific order. One of the most straightforward algorithms used for sorting is the Bubble Sort algorithm.
Bubble sort is a sorting algorithm that compares adjacent elements in a list or an array and swaps them if they are in the wrong order. If there are numbers smaller than the current element at a particular index, they will be swapped. This process is repeated until the list or array is completely sorted.
The name “bubble sort” comes from the way the algorithm works. The largest element, “bubble” to the end of the list, just like bubbles, rises to the water’s surface.
Bubble Sort is one of the simplest sorting algorithms to understand and implement. However, it is not very efficient and can be slow for large datasets.
In this article, we will discuss the Bubble Sort Algorithm in detail, its advantages and disadvantages, its time and space complexity, and how to implement Bubble Sort Programs in C, C++, C#, Java, Python, and PHP.
Table of Contents
- 1 How does Bubble Sort Work?
- 2 How to Implement Bubble Sort in C#?
- 3 Advantages of Bubble Sort Algorithm
- 4 Disadvantages of Bubble Sort Algorithm
- 5 Bubble Sort Performance
- 6 How does Bubble Sort Work?
- 7 Bubble Sort Program in C
- 8 Bubble sort program in C++
- 9 Bubble Sort Program in Java
- 10 Code Explanation:
- 11 Bubble Sort Program in Python
- 12 FAQs:
- 12.1 Q: What is the Bubble Sort algorithm?
- 12.2 Q: What are the advantages of using the Bubble Sort algorithm?
- 12.3 Q: What are the disadvantages of using the Bubble Sort algorithm?
- 12.4 Q: How does Bubble Sort compare to other sorting algorithms?
- 12.5 Q: When should I use the Bubble Sort algorithm?
- 12.6 Related
How does Bubble Sort Work?
Bubble sort works by repeatedly swapping adjacent elements that are in the wrong order. It begins by comparing the first two elements of the list. If the first element is greater than the second, they are swapped.
The algorithm then moves on to compare the second and third elements, and so on, until it reaches the end of the list.
After the first pass, the largest element will be placed at the end of the list. The algorithm then repeats the process for the remaining elements, swapping them until the list is sorted.
How to Implement Bubble Sort in C#?
The implementation of the Bubble Sort Algorithm in C# is straightforward. Here is a sample code that demonstrates the Bubble Sort in C#:
using System;
class BubbleSortProgram
{
static void Main()
{
int[] arr = { 10, 50, 20, 40, 30 };
BubbleSort(arr);
Console.WriteLine("Sorted array:");
for (int i = 0; i < arr.Length; i++)
{
Console.Write(arr[i] + " ");
}
Console.ReadKey();
}
static void BubbleSort(int[] arr)
{
int n = arr.Length;
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
// swap arr[j] and arr[j+1]
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
}
Output:
Sorted array:
10 20 30 40 50
Code explanation:
In the above Bubble sort program, we have defined an array of integers with values { 10, 50, 20, 40, 30 }. Then the BubbleSort() method is called, which takes an array as input and performs the bubble sort algorithm using nested for-loops.
The outer loop iterates from the first element of the array to the second to last element. The inner loop iterates from the first element of the array to the last unsorted element.
In each inner loop iteration, the current element is compared with the next element. Suppose the current element is greater than the next element. In that case, they are swapped. This process will continue until the end of the array is reached.
Understanding the Sorting Process of Bubble Sort Algorithm
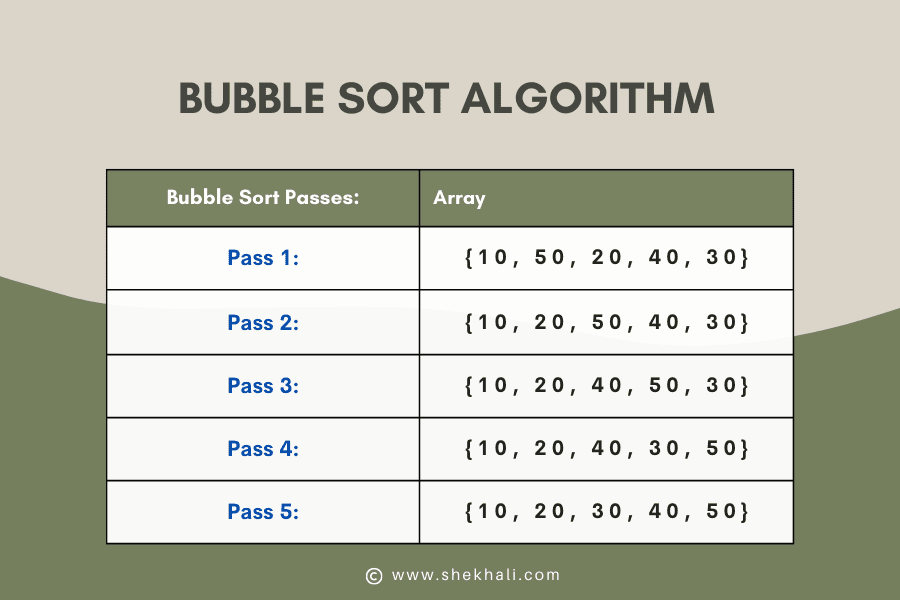
Bubble sort operates through a series of passes, where each pass compares two adjacent numbers and swaps them if they are in the wrong order. If there are N numbers in the data set, then the number of passes needed to sort the data set is N – 1. During each pass, the two numbers are compared, and the sequence is repeated until all numbers are sorted in the desired manner.
Here is an example of Bubble Sort using the array of the above program ({10, 50, 20, 40, 30}). Here we will understand each phase of the sorting process:
| Bubble Sort Sorting Passes: | Array |
|---|---|
| Pass 1: | {10, 50, 20, 40, 30} |
| Pass 2: | {10, 20, 50, 40, 30} |
| Pass 3: | {10, 20, 40, 50, 30} |
| Pass 4: | {10, 20, 40, 30, 50} |
| Pass 5: | {10, 20, 30, 40, 50} |
- In the first pass, the bubble sort algorithm compares the first two elements of the array and swaps them if the first element is greater than the second element. In this case, 10 is not greater than 50, so the array remains the same.
- In the second pass, the algorithm compares the second and third elements of the array and swaps them if the second element is greater than the third element. In this case, 50 is greater than 20, so they are swapped, resulting in {10, 20, 50, 40, 30}.
- In the third pass, the algorithm compares the third and fourth elements of the array and swaps them if the third element is greater than the fourth element. In this case, 50 is greater than 40, so they are swapped, resulting in {10, 20, 40, 50, 30}.
- In the fourth pass, the algorithm compares the fourth and fifth elements of the array and swaps them if the fourth element is greater than the fifth element. In this case, 50 is greater than 30, so they are swapped, resulting in {10, 20, 40, 30, 50}.
- In the fifth and final pass, the algorithm repeats the previous steps until no more swaps are necessary. In this case, no more swaps are necessary, so the algorithm is complete and the sorted array is {10, 20, 30, 40, 50}.
Advantages of Bubble Sort Algorithm
The advantages of using the Bubble Sort algorithm are:
- Simplicity: Bubble Sort is one of the simplest sorting algorithms to understand and implement.
- Memory efficient: It does not require any additional memory other than the array that is being sorted.
- Good for small data sets: Bubble Sort is an efficient algorithm for small data sets where the amount of data to be sorted is not very large.
- Easy to optimize: It is easy to optimize the Bubble Sort algorithm for better performance by using techniques like early termination, adaptive bubble sort, and flagging.
Disadvantages of Bubble Sort Algorithm
The disadvantages of using the Bubble Sort algorithm are as follows:
- Time complexity: Bubble Sort has a time complexity of O(n^2), meaning its efficiency decreases as the number of elements to be sorted increases.
- Inefficient for large datasets: Bubble Sort is not recommended for large datasets as it takes a long time to sort them.
- Not suitable for real-time applications: Bubble Sort is not suitable for real-time applications as it takes a lot of time to sort the data.
- Not stable for duplicate elements: Bubble Sort is not a stable sorting algorithm, meaning the order of duplicate elements may not be preserved after sorting.
- Not optimal for almost sorted data: If the data is already sorted or nearly sorted, the Bubble Sort algorithm may still iterate through all passes, which is an unnecessary waste of time.
Bubble Sort Performance
The time complexity of the bubble sort algorithm is O(n^2), where ‘n’ is the number of elements in the array. It means that the time taken to sort the array increases exponentially with the number of elements.
In terms of space complexity, bubble sort is an in-place sorting algorithm, which means that it requires only a constant amount of additional space to sort the array.
Although bubble sort is easy to understand and implement, it is not the most efficient sorting algorithm, especially for large datasets. In fact, bubble sort is considered one of the slowest sorting algorithms and is rarely used in practical applications.
How does Bubble Sort Work?
Bubble sort works by repeatedly swapping adjacent elements in the array if they are in the wrong order. The algorithm starts from the beginning of the array and compares each element with the next one. If the current element is greater than the next element, they are swapped. The algorithm then moves on to the next pair of elements and repeats the process until the entire array is sorted.
The sorting process is repeated multiple times, with each pass through the array sorting one additional element. In each pass, the largest unsorted element “bubbles up” to its correct position at the end of the array.
Bubble Sort Program in C
Here is an implementation of the bubble sort algorithm in C.
#include <stdio.h>
void bubbleSort(int arr[], int n) {
int i, j;
for (i = 0; i < n-1; i++) {
for (j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
int main() {
int arr[] = {10, 50, 20, 40, 30};
int n = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, n);
printf("Sorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
This program sorts the array {10, 50, 20, 40, 30} using the bubble sort algorithm and outputs the sorted array {10, 20, 30, 40, 50}.
Bubble sort program in C++
#include <iostream>
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
int main() {
int arr[] = {10, 50, 20, 40, 30};
int n = sizeof(arr)/sizeof(arr[0]);
bubbleSort(arr, n);
std::cout << "Sorted array: ";
for (int i = 0; i < n; i++) {
std::cout << arr[i] << " ";
}
std::cout << std::endl;
return 0;
}
Output:
Sorted array:
10 20 30 40 50
Bubble Sort Program in Java
Here is a simple implementation of the Bubble Sort algorithm in Java, with explaining each step:
public class BubbleSortProgram {
public static void main(String[] args) {
int[] arr = { 10, 50, 20, 40, 30 };
bubbleSort(arr);
System.out.println("Sorted array:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
public static void bubbleSort(int[] arr) {
int n = arr.length;
for (int i = 0; i < n-1; i++) {
for (int j = 0; j < n-i-1; j++) {
if (arr[j] > arr[j+1]) {
// Swap arr[j] and arr[j+1]
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
}
Output:
Sorted array:10 20 30 40 50
Code Explanation:
In this program, we first define an array of integers arr with some unsorted values. We then call the bubbleSort() function to sort the array using the Bubble Sort algorithm.
The bubbleSort() function takes an array as an argument and performs the sorting operation on it. It works by iterating over the array using two nested loops. The outer loop runs from 0 to n-1, where n is the length of the array. The inner loop runs from 0 to n-i-1, where i is the current iteration of the outer loop. This inner loop compares adjacent elements of the array and swaps them if they are not in the correct order.
The swapping is done using a temporary variable temp. If the value of arr[j] is greater than that of arr[j+1], then the two values are swapped. Once all the iterations are completed, the array is sorted in ascending order.
Bubble Sort Program in Python
Here is an implementation of the Bubble Sort algorithm in Python:
def bubbleSort(arr):
n = len(arr)
for i in range(n-1):
for j in range(0, n-i-1):
if arr[j] > arr[j+1] :
# Swap arr[j] and arr[j+1]
arr[j], arr[j+1] = arr[j+1], arr[j]
arr = [10, 50, 20, 40, 30]
bubbleSort(arr)
print ("Sorted array:")
for i in range(len(arr)):
print(arr[i])
Output:
Sorted array:
10
20
30
40
50
References:WikiPedia-Bubble Sort
FAQs:
Here are some FAQs about Bubble Sort:
Q: What is the Bubble Sort algorithm?
Bubble Sort is a simple sorting algorithm that repeatedly compares and swaps adjacent elements in an array or list until they are in the correct order.
Q: What are the advantages of using the Bubble Sort algorithm?
The main advantage of using Bubble Sort is its simplicity and ease of implementation. It is also useful for sorting small datasets.
Q: What are the disadvantages of using the Bubble Sort algorithm?
The main disadvantage of using Bubble Sort is its inefficiency for large datasets. It has a time complexity of O(n^2), which can result in slow sorting times.
Q: How does Bubble Sort compare to other sorting algorithms?
Bubble Sort is one of the slowest sorting algorithms and is generally not used for large datasets. Other sorting algorithms, such as Merge Sort, Quick Sort, and Heap Sort, perform better for larger datasets.
Q: When should I use the Bubble Sort algorithm?
Bubble Sort is a simple sorting algorithm that works well for small datasets. However, it has a time complexity of O(n^2), which makes it inefficient for larger datasets. Therefore, it is recommended to use Bubble Sort only for small datasets. More efficient algorithms such as Quick Sort, Merge Sort, or Heap Sort should be used for larger datasets.
Articles you might also like:
- Program to copy all elements of an array into another array
- Leap Year program in C, C++, C#, JAVA and Python
- Program to print prime numbers from 1 to N
- Different Ways to Calculate Factorial in C# (with Full Code Examples)
- Fibonacci sequence: Fibonacci series in C# (with examples)
- Program to Convert Fahrenheit to Celsius: Algorithm, Formula, and Code Examples
- Converting Celsius to Fahrenheit in C#
- Different Ways to Calculate Factorial in C# (with Full Code Examples)
- Difference Between Array And ArrayList In C#: Choosing the Right Collection - May 28, 2024
- C# Program to Capitalize the First Character of Each Word in a String - February 21, 2024
- C# Program to Find the Longest Word in a String - February 19, 2024